機械の動き

往復運動と回転運動

古くは水車が回転する力を利用して石臼を突く杵の動きのように、機械には、回転運動を往復運動に変換（またはその逆）する仕組みが多く見られます。
ここではその仕組みを解説したアニメーションの例を紹介しています。

蒸気機関車の動力のしくみ

蒸気機関車の動輪を回転させる仕組みを紹介しています。
石炭を燃やして熱せられた水蒸気がピストンを押し、その圧力が動輪を回転させる力になります。
また同時に弁を移動させて、水蒸気をシリンダーの反対側の空間に送り込み、ピストンを逆方向に動かす力を発生させます。この繰り返しにより、水蒸気が送られる間は動輪は回転を続けます。
このように、見えない機械の内部の仕組みを説明したり、物理的な法則を可視化したりする手段としてもアニメーションは威力を発揮します。

※このアニメーションは、筆者が日本テレビ「所さんの目がテン！」のために制作したものを利用しています。

回転運動を往復運動に変換する装置

ここではYouTubeに上がっていた二本のムービーを紹介します。
最初の「回転運動を直線運動に変換するしくみ」では、クランクや歯車、ネジやシリンダーなど様々な道具を使って回転運動を往復運動に変える装置を3DCGで分かりやすく説明しています。
「グラスホフの定理適用のメカニズム」も、回転運動を往復運動に変える装置をとりあげていますが、「グラスホフの定理」の適用例として紹介しています。 4本の棒が回転可能な関節でつながれている機械システムを「4 バーリンクシステム」と言い、この研究での基本原則が「グラスホフの法則」です。グラスホフの定理は、4つのリンクの長さと関節の配置に基づいて、システムがどのように動作するかを予測するのに使われます
下のタイトルをクリックしてご覧ください。　

・「回転運動を直線運動に変換するしくみ」

・「グラスホフの定理適用のメカニズム - 機械的原理」

※ このムービーは、YouTubeにリンクして表示しています。YouTubeで削除された場合は表示されないことがありますが、その場合はご容赦ください。　

グラスホフの定理について

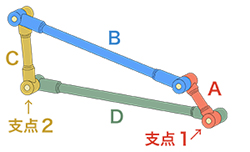
グラスホフの定理は、四つの棒ABCDがそれぞれ蝶番（ちょうつがい）で連結されている場合の、それぞれの運動と機械的制約を説明したものです。もっとも短い棒Aが1回転するための条件は，次の3つの式を同時に満たすことであるとされています。 A+B ≦ C+D、A+C ≦ B+D、A+D ≦ B+C
左図の例では、Aが支点1を中心にして回転運動をすると、Cはそれに伴って支点2を中心に円弧を描くように往復運動をします。